Answer
Question A:
The answer is Inverse
Question B:
The answer is Converse
Question C:
The answer is Contrapositive
SOLUTION
Problem Statement
The question gives us a statement and we are asked to find its inverse, converse, and contrapositive. The statement given is:
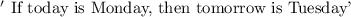
Method
To solve this question, we need to know the definitions for each of inverse, converse, contrapositive.
Given the original statement, "If p, then q"
Inverse:
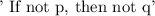
Converse

Contrapositive:
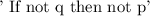
With these definitions, we can solve the question.
Implementation
Let p be "today is Monday".
Let q be "tomorrow is Tuesday"
Thus, the original statement can be written as:
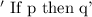
Question A:
If today is not Monday, then tomorrow is not Tuesday.
If p is "today is Monday" and q is "tomorrow is Tuesday"
Then, we can re-write the statement as follows:
"if not p then not q"
This corresponds to Inverse
Question B:
"If tomorrow is Tuesday, then today is Monday."
This can be re-written as:
"If q, then p"
This corresponds to Converse
Question C:
"If tomorrow is not Tuesday, then today is not Monday"
This can be re-written as:
"if not q, then not p"
This corresponds to Contrapositive
Final Answer
Question A:
The answer is Inverse
Question B:
The answer is Converse
Question C:
The answer is Contrapositive