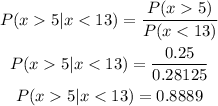Question

I need help to figure out why in Part F it was 0.8889 and I need help with G,H

Answer 1

QUESTION G:

To find the 91st percentile, we use the formula:

`p=(x-l)/(h-l)`

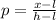
where

`\begin{gathered} p=\text{ percentile} \\ l=\text{lowest value} \\ h=\text{ highest value} \\ x=91st\text{ percentile value} \end{gathered}`

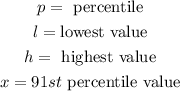
From the question, we have:

`\begin{gathered} l=4 \\ h=36 \\ p=(91)/(100)=0.91 \end{gathered}`

Therefore, we can calculate the value for x to be:

`\begin{gathered} 0.91=(x-4)/(36-4) \\ 0.91=(x-4)/(32) \\ x-4=32*0.91 \\ x-4=29.12 \\ x=29.12+4 \\ x=33.12 \end{gathered}`

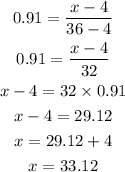
Therefore, the 91st percentile is 33.12

QUESTION H:

The lower quarter is the bottom 25% of the numbers.

The maximum of the bottom quarter is the 25th percentile.

Using the formula from the previous part, where x is now the 25th percentile value, we have the following parameters:

`\begin{gathered} p=(25)/(100)=0.25 \\ l=4 \\ h=36 \end{gathered}`

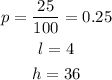
Therefore, the 25th percentile is calculated to be:

`\begin{gathered} 0.25=(x-4)/(36-4) \\ 0.25=(x-4)/(32) \\ x-4=0.25*32 \\ x-4=8 \\ x=8+4 \\ x=12 \end{gathered}`

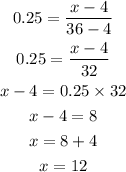
Therefore, the maximum value of the lower quarter is 12.

QUESTION F:

To calculate the probability that x > 5 given that x < 13, we can use the formula:

`P=(x_2-x_1)/(h-l)`

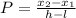
where, for x > 5

`\begin{gathered} x_2=13 \\ x_1=5 \\ h=36 \\ l=4 \end{gathered}`

Substituting into the formula, we have:

`P(x>5)=(13-5)/(36-4)=0.25`

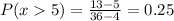
and for x < 13

`\begin{gathered} x_2=13 \\ x_1=4 \end{gathered}`

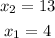
Therefore:

`P(x<13)=(13-4)/(32)=0.28125`

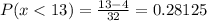
Combining the probabilities, we have:

`\begin{gathered} P(x>5|x<13)=(P(x>5))/(P(x<13)) \\ P(x>5|x<13)=(0.25)/(0.28125) \\ P(x>5|x<13)=0.8889 \end{gathered}`