Question

Show the sine, cosine, and tan of the given triangle

Answer 1

Trigonometry

We have that the sides of a right triangle receive different names depending on the angle we are going to analyze.

The opposite side of the right triangle is the hypotenuse:

And depending on the angle we are going to analyze, one side is that opposite to it and the other side is the adjacent:

Finding the missing side

We know by the Pythagorean Theorem that:

opposite² + adjacent² = hypotenuse²

In this case

hypotenuse = 20

adjacent = 16

opposite BC

Then

opposite² + adjacent² = hypotenuse²

↓

BC² + 16² = 20²

↓

BC² = 20² - 16²

BC² = 144 = 12²

↓

BC = 12

Sine

We have that the Sine formula is:

`\sin (\text{angle)}=\frac{\text{opposite}}{\text{hypotenuse}}`

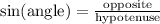
In this case:

angle = A

opposite side = 12

hypotenuse = 20

Then,

`\begin{gathered} \sin (\text{angle)}=\frac{\text{opposite}}{\text{hypotenuse}} \\ \downarrow \\ \sin A=\frac{\text{1}2}{\text{2}0} \end{gathered}`

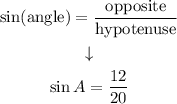
If we simplify it, we have:

`\sin A=\frac{\text{1}2}{\text{2}0}=(3)/(5)=0.6`

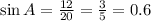
Cosine

We have that the Cosine Formula is:

`\cos (\text{angle)}=\frac{\text{adjacent}}{\text{hypotenuse}}`

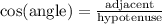
In this case:

angle = A

adjacent side = 16

hypotenuse = 20

Then

`\begin{gathered} \cos (\text{angle)}=\frac{\text{adjacent}}{\text{hypotenuse}} \\ \downarrow \\ \cos A=(16)/(20) \end{gathered}`

If we simplify it, we have:

`\cos A=\frac{\text{1}6}{\text{2}0}=(4)/(5)=0.8`

Tangent

We have that the Tangent Formula is:

`\tan (\text{angle)}=\frac{\text{opposite}}{\text{adjacent}}`

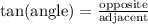
In this case:

angle = A

opposite side = 12

adjacent side = 16

`\begin{gathered} \tan (\text{angle)}=\frac{\text{opposite}}{\text{adjacent}} \\ \downarrow \\ \tan A=(12)/(16) \end{gathered}`

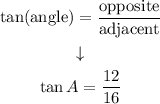
If we simplify it, we have:

`\tan A=(3)/(4)=0.75`

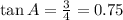
Answers

sinA = 0.6

cosA = 0.8

tanA = 0.75