Question

Solve the following system of equations using an inverse matrix. You must alsoindicate the inverse matrix, A-1, that was used to solve the system. You mayoptionally write the inverse matrix with a scalar coefficient.4x+9y = -1-3x-9y = 2

Answer 1

We are given a set of equations and we want to solve them using the matrix inverse. To do so, first, we write the system of equations, which is

`\begin{gathered} 4x+9y=\text{ -1} \\ \text{ -3x -9y= 2} \end{gathered}`

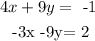
Now, we will write the system of equations in a matrix form. That is, we will write a matrix, such that the product of the matrix and a vector will lead to the system of equations. We write it as

`\begin{bmatrix}{4} & {9} \\ {\text{ -3}\placeholder{⬚}} & \text{ -9}{\placeholder{⬚}}\end{bmatrix}\cdot\begin{bmatrix}{x} & {\placeholder{⬚}} \\ {y} & {\placeholder{⬚}}\end{bmatrix}=\begin{bmatrix}{\placeholder{⬚}\text{ -1}} & {\placeholder{⬚}} \\ {2} & {\placeholder{⬚}}\end{bmatrix}`

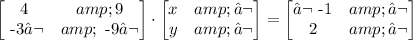
so the matrix A would be

`A=\begin{bmatrix}{4} & {9} \\ {\placeholder{⬚}\text{ -3}} & {\placeholder{⬚}\text{ -9}}\end{bmatrix}`

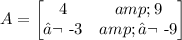
Now, we use some help to calculate the inverse of A (the explanation on how to calculate the inverse is beyond the scope of the question). So, we have

`A^{\placeholder{⬚}\text{ -1}}=\begin{bmatrix}{1} & {1} \\ {\frac{\text{ -1}}{3}} & {\frac{\placeholder{⬚}\text{ -4}}{9}}\end{bmatrix}`

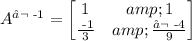
so, to solve the problem, we multiply the inverse matrix of A on the right side of both sides of the equation. So we have

`\begin{bmatrix}{x} & {\placeholder{⬚}} \\ {y} & {\placeholder{⬚}}\end{bmatrix}=\begin{bmatrix}{1} & {1} \\ {\frac{\text{ -1}}{3}} & {\text{ }\frac{\text{ -4}}{9}}\end{bmatrix}\cdot\begin{bmatrix}{\text{ -1}} & {\placeholder{⬚}} \\ {2} & {\placeholder{⬚}}\end{bmatrix}=\begin{bmatrix}{1} & {\placeholder{⬚}} \\ {\frac{\text{ -5}}{9}} & {\placeholder{⬚}}\end{bmatrix}`

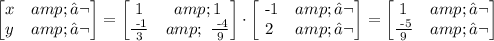
so x=1 and y= -5/9