Question

Joe Kelly 4 hours miles 2. Joe and Kelly each leave for a hike at the same time, but they walk at different paces. Joe's data is shown in a table and Kelly's data is shown in a graph. Time (h) Distance (mi) 20 2 3 6 How long does it take Joe to hike one mile? Distance (mi) 10 6 9 8 12 O How long does it take Kelly to hike one mile? 20 10 Time (h) Who is hiking faster? How do you know?

Answer 1

From the table, Joe takes 2 hours to hike 3 miles. To find how long does it take Joe to hike 1 mile, we can use the next proportion,

`\frac{2\text{ hours}}{x\text{ hours}}=\frac{3\text{ miles}}{1\text{ mile}}`

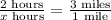
Solving for x,

`\begin{gathered} 2\cdot1=3\cdot x \\ (2)/(3)=x \end{gathered}`

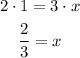
Joe takes 2/3 hours to hike 1 mile.

From the graph, Kelly takes 12 hours to hike 10 miles. To find how long does it take Kelly to hike 1 mile, we can use the next proportion,

`\frac{12\text{ hours}}{x\text{ hours}}=\frac{10\text{ miles}}{1\text{ mile}}`

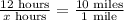
Solving for x,

`\begin{gathered} 12\cdot1=10\cdot x \\ (12)/(10)=x \\ (6)/(5)=x \end{gathered}`

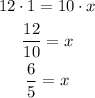
Kelly takes 6/5 hours to hike 1 mile.

Joe is hiking faster, because he hikes 1 mile in less time than Kelly