Question

Calculate the beat frequencies that are heard when the following pairs of frequencies are sounded together:A. 312 Hz and 300 HzB. 852 Hz and 857 HzC. 1024 Hz and 1000 Hz

Answer 1

`\begin{gathered} f_(b(A))=12\text{ Hz} \\ f_(b(B))=5\text{ Hz} \\ f_(b(C))=24\text{Hz} \end{gathered}`

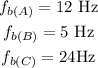
Step-by-step explanation

The beat frequency is equal to the complete value of the alteration in the frequency of the two waves. The count of beats per second is equivalent to the difference in frequencies of two waves is called beat frequency.

it is given by the expression:

`\begin{gathered} f_b=\lvert f_2-f_1\rvert \\ \text{where} \\ f_b\text{ is }beat\text{ frequency} \\ f_1\text{ is frequency of first wave } \\ f_2\text{ is frequency of second wave} \end{gathered}`

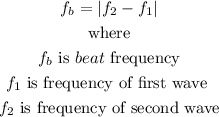
then

Step 1

let

`\begin{gathered} f_1=312\text{ Hz} \\ f_2=300\text{ Hz} \end{gathered}`

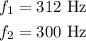
now,replace

`\begin{gathered} f_b=\lvert f_2-f_1\rvert \\ f_b=\lvert(300-312)Hz\rvert \\ f_b=\lvert-12Hz\rvert \\ f_(b(A))=12\text{ Hz} \end{gathered}`

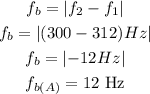
Step 2

do, the same for the same pair of frequencies

let

`\begin{gathered} f_1=852\text{Hz} \\ f_2=857\text{ Hz} \end{gathered}`

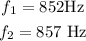
now,replace

`\begin{gathered} f_b=\lvert f_2-f_1\rvert \\ f_b=\lvert(857-852)Hz\rvert \\ f_b=\lvert5Hz\rvert \\ f_(b(B))=5\text{ Hz} \end{gathered}`

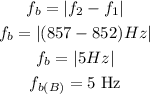
Step 3

the last pair of frequencies:

let

`\begin{gathered} f_1=1024\text{Hz} \\ f_2=1000\text{Hz} \end{gathered}`

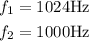
now,replace

`\begin{gathered} f_b=\lvert f_2-f_1\rvert \\ f_b=\lvert(1000-1024)Hz\rvert \\ f_b=\lvert-24Hz\rvert \\ f_(b(C))=24\text{Hz} \end{gathered}`

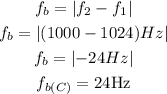
I hope this helps you