Question

How do I solve the Average Rate of Change?Problem:f(x)=x^2+5x-12 -> (-2, 5)

Answer 1

Step-by-step explanation

The average rate of change of a given function f(x) in the interval (a,b) is given by the following formula:

`AROC=(f(b)-f(a))/(b-a)`

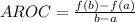
This is valid only if f(x) is defined at x=a and x=b.

In our case the interval is (-2,5) and the function is:

`f(x)=x^2+5x-12`

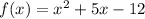
So we need to find f(-2) and f(5):

`\begin{gathered} f(-2)=(-2)^2+5\cdot(-2)-12=-18 \\ f(5)=5^2+5\cdot5-12=38 \end{gathered}`

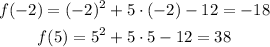
Then the average rate of change of this function in the interval (-2,5) is given by:

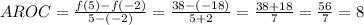
`AROC=(f(5)-f(-2))/(5-(-2))=(38-(-18))/(5+2)=(38+18)/(7)=(56)/(7)=8`Answer

Then the answer is that the Average Rate of Change of f(x) in (-2,5) is 8.