Given the points below,
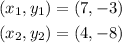
The formula to find the equation of a straight line is given below as,
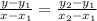
Substituting the variables into the formula of a straight line above,
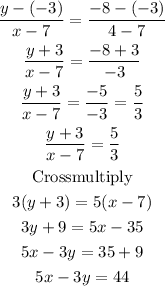
The standard form of a straight is given as Ax + By = C
Hence, the answer is 5x -3y = 44