In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data:
AT = 10
∠ ADT = 45°
Step 02:
right triangle (isosceles triangle):
we must analyze the figure to find the solution.
AT = opposite
AD = adjacent
TD = hypotenuse
sin α = opposite / hypotenuse
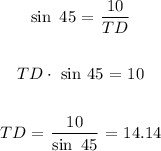
cos α = adjacent / hypotenuse

∠ TAD = 90°
∠ ATD = (180 - 90 - 45)° = 45°
The answer is:
∠ ADT = 45°
∠ TAD = 90°
∠ ATD = 45°
AT = 10
TD = 14.14
AD = 10