Question

consider the discrete random variable x given in the table below calculate the mean variance and standard deviation of X also calculate the expected value of x round solution to three decimal places if necessary

Answer 1

We have a table for the probability distribution P(X) for the discrete variable x.

1) We must calculate the mean value μ of the variable x, using the following formula and the data from the table we have:

`\begin{gathered} E(x)=\mu=\sum ^{}_ix_i\cdot P(x_i) \\ \mu=1\cdot P(x=1)+6\cdot P(x=6)+11\cdot P(x=11)+15\cdot P(x=15)+18\cdot P(x=18) \\ \mu=1\cdot0.07+6\cdot0.07+11\cdot0.08+15\cdot0.09+18\cdot0.69 \\ \mu=15.14 \end{gathered}`

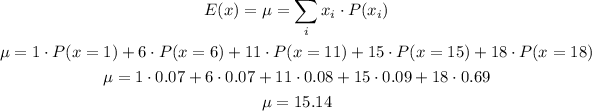
2) We must calculate the variance σ² of the variable x, using the following formula and the data from the table we have:

`\begin{gathered} \sigma^2=\sum ^{}_i(x_i-\mu)^2\cdot P(x_i) \\ \sigma^2=(1-\mu)^2\cdot P(1)+(6-\mu)^2\cdot P(6)+(11-\mu)^2\cdot P(11)+(15-\mu)^2\cdot P(15)+(18-\mu)^2\cdot P(18) \\ \sigma^2=26.8604 \\ \sigma^2\cong26.860 \end{gathered}`

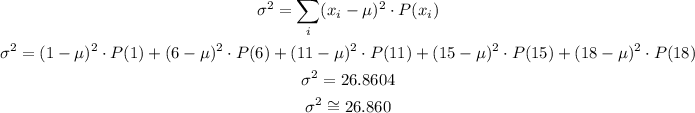
3) We calculate the standard deviation σ of the variable x simply taking the square root of the variance σ²:

`\begin{gathered} \sigma=\sqrt[]{\sigma^2} \\ \sigma=\sqrt[]{26.8604} \\ \sigma\cong3.891 \end{gathered}`

4)