Question

Need help writing the equation of the line in fully simplified slope-intercept form

Answer 1

y=4x-5

Step-by-step explanation

the slope -intercept form of the equation of a line is

`\begin{gathered} y=mx+b \\ where\text{ m is the slope and b is the y-intercept} \end{gathered}`

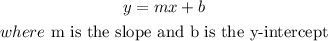
so

Step 1

find the slope of the line

we can find the slope of a line using the formula

`\begin{gathered} slope=\frac{change\text{ in y}}{change\text{ in x}}=(y_2-y_1)/(x_2-x_1) \\ where \\ P1(x_1,y_1) \\ and \\ P2(x_2,y_2)\text{ are 2 points from the line} \end{gathered}`

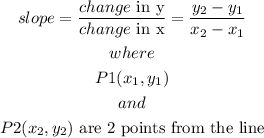
so

a) let

`\begin{gathered} P1(-1,-1) \\ P2(0,-5) \end{gathered}`

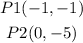
b) now, replace in the formula

`\begin{gathered} slope\frac{}{}=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ slope=(-5-(-1))/(0-(-1))=(-5+1)/(1)=-4 \end{gathered}`

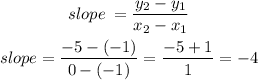
Step 2

y-intercept:

now, to find the value of b ( y-intercpet) we need to check in the graph , the point where the lines crosses the y-axis and take the y-coordinate, so

so

b=-5

Step 3

finally, replace

`\begin{gathered} y=mx+b \\ y=-4x-5 \end{gathered}`

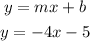
so, the equation of the line is

y=-4x-5