Question

A rectangle garden has a total area of 48 square yards..draw and label two possible rectangular gardens with different side lengths that have the same area,so now which one of my designs will require less fencing

Answer 1

What we want to do is find multiple solutions that accommodate better the following function:

`l\cdot h=48`

Such that the following has the smallest value possible:

`2l+2h=p`

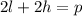
Where p is the total fencing.

*We solve by finding multiples of 48, those being: 1, 2, 3, 4, 6, 8, 12, 16, 24 & 48.

From this, we will have that the possible lengths and heights are:

1 x 48

2 x 24

3 x 16

4 x 12

6 x 8

We determine which rectangles are by adding the sides and determining which one is the smallest value, that is:

2(1) + 2(48) = 98

2(2) + 2(24) = 52

2(3) + 2(16) = 38

2(4) + 2(12) = 32

2(6) +2(8) =