Question

y = x + 6BAA. The slope of line CD is 5/3.B. The slope of line CD is 6.DThese triangles aresimilar. The equationfor line AB is given.What is the slope ofline CD?

Answer 1

We are told that both triangles are similar. Recall that the sides of a rigth triangle are called legs and hypotenuse. The legs are the sides that form a right angle (90°).

As we are told that both triangles are similar, we must have that the ratio of legs from the left most triangle should be the same ratio as the ratio from the legs of the right side triangle.

In this case, consider the ratio of the longest leg and the shortest leg. That is

`\frac{longest\text{ leg}}{shortest\text{ leg}}`

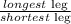
If we calculate it for the left most triangle, we can see that, by definition, it is the slope of the given line. So we have

`\frac{longest\text{ leg left triangle}}{shortest\text{ leg left triangle}}=(5)/(3)`

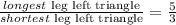
as both triangles are similar, we should have that

`\frac{longest\text{ leg right triangle}}{shortest\text{ leg right triangle}}=\frac{longest\text{ leg left triangle}}{shortest\text{ leg left triangle}}=(5)/(3)`

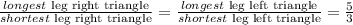
but note again that the ratio of the longest leg of the right triangle and the shortest leg of the right triangle is the slope of the second line. So the slope of line CD is 5/3