Question

Shelby puts 600.00 into an account to use for school expenses the account earns 10% interest compounded quarterly how much will be in the account after 9 years

Answer 1

Answer:

1460 will be in the account after 9 years

Explanations:

Let the amount put into the account be P

P = 600.00

The interest rate, r = 10% = 0.1

The number of years, t = 9

The interest is compounded quarterly

There are four quarters in a year, n = 4

The amount, A, in the account at the end of the 9 years will be given by the formula:

`\begin{gathered} \text{A = P(1 + }(r)/(n))^(nt) \\ \end{gathered}`

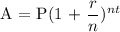
Substitute the value of P, r, t, and n into the formula:

`\begin{gathered} A\text{ = 600(1 + }(0.1)/(4))^(4(9)) \\ A\text{ = 600(1 + }0.025)^(36) \\ A=600(1.025)^(36) \\ A\text{ = 600(}2.433) \\ A\text{ = }1459.8 \end{gathered}`

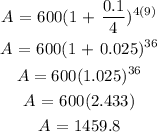
1460 will be in the account after 9 years