Interquartile range is equal to the difference between the 75th percentile and 25th percentile, including in its interval 50% of the data.
If x is normally distributed, we have to calculate the z-value that includes 25% of the data, so that 50% of the data is within -z and z (in standard form).
The value of z that includes 50% of the data is z=+/- 0.6745
Then, we can calculate the limits of x as:
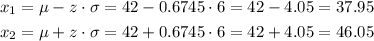
The interquartile range is [37.95, 46.05].