Given:
A swimming pool is in the form of a semicircular-sided figure
Required:
What is the area of the 3 ft wide surrounding the pool?
Step-by-step explanation:
We will find area as:
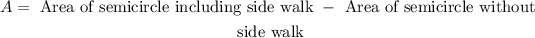
Now, radius for smaller semicircle is 5 ft and radius for larger semicircle (5 + 3 = 8)
So,

If we take walk on both sides, we will multiply it with 2
A = 2*61.23
A = 122.46 ft square
Now, we have one side of bigger rectangle is 10 + 3 + 3 = 16 ft
So,
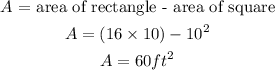
Finally,
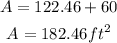
Answer:
Hence, above is the answer.