Question

Which is better if the interest rate is 5%: $1000 now or $1100 in two years time?

Answer 1

Let's calculate how much will the $1,000 will be worth after earning 5% interest in two years.

Remember that to calculate the future value we use the formula:

`FV=P(1+r)^n`

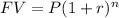
Where:

• FV, is the future value

,

• P, is the initial amount invested

,

• r, is the interest rate

,

• n, is the number of years

Using the data we have, we'll get:

`FV=1000(1+(5)/(100))^2=1102.5`

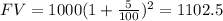
Thereby, we can conclude that it would be better to take the $1,000 now and invest the money at a 5% interest rate for two years rather than getting $1,100 in two years time.