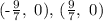Question

Find the vertices and foci of the ellipse.49x^2 = 81 - 81y^2

Answer 1

Given the following equation of an ellipse:

`49x^2=81-81y^2`

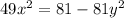
The standard form equation of an ellipse is:

`\text{ }((x-h)^2)/(a^2)\text{ + }((y-k)^2)/(b^2)\text{ = }1`

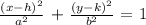
Where (h, k) is the center, a and b are the lengths of the semi-major and the semi-minor axis.

Let's transform it into the standard form:

`49x^2=81-81y^2`
`49x^2+81y^2=81`
`(49x^2+81y^2=81)/(81)`
`(49x^2)/(81)+(y^2)/(1)=1`
`(x^2)/((81)/(49))+(y^2)/(1)=1`
`\frac{(x-0)^2^{}}{(81)/(49)}+\frac{(y-0)^2^{}}{1}=1`
`((x-0)^2)/(((9)/(7))^2)+((y-0)^2)/(1)=1`

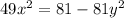
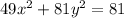
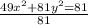
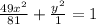
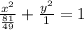
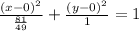
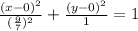
From this equation, we get:

`\begin{gathered} \text{ h = 0} \\ \text{ k = 0} \\ \text{ a}^2\text{ = }(81)/(49)\text{ }\rightarrow\text{ a = }\sqrt[]{(81)/(49)}\text{ }\rightarrow\text{ a = }(9)/(7) \\ \text{ }b^2\text{ = 1 }\rightarrow\text{ b= }\sqrt[]{1}\text{ }\rightarrow\text{ b = 1} \end{gathered}`

For c,

`\text{ c = }\sqrt[]{a^2-b^2}\text{ = }\sqrt[]{((9)/(7))^2\text{ - 1}}\text{ = }\sqrt[]{(81)/(49)\text{ - 1}}\text{ = }\sqrt[]{(81)/(49)-(49)/(49)}\text{ = }\sqrt[]{(32)/(49)}\text{ = }\frac{4\sqrt[]{2}}{7}`

Let's now get the foci of the ellipse:

The first focus: (h - c, k)

`\text{ (h - c, }k)\text{ = (0 - }\frac{4\sqrt[]{2}}{7},\text{ 0)}`
`\text{ (h - c, }k)\text{ = (-}\frac{4\sqrt[]{2}}{7},\text{ 0)}`

The second focus: (h + c, k)

`\mleft(h+c,k\mright)\text{ = (0 + }\frac{4\sqrt[]{2}}{7},\text{ 0)}`
`(h+c,k)\text{ = (}\frac{4\sqrt[]{2}}{7},\text{ 0)}`

Next, let's find the vertices:

The first vertex: (h − a, k)

`\text{ (h - a, k) = }(0\text{ - }(9)/(7),\text{ 0)}`
`\text{ (h - a, k) = }(\text{-}(9)/(7),\text{ 0)}`

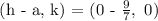
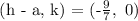
The second vertex: (h + a, k)

`\text{ (h + a, k) = }(0+(9)/(7),\text{ 0)}`
`\text{ (h + a, k) = }((9)/(7),\text{ 0)}`

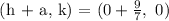
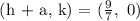
In Summary:

Therefore, in an ellipse with the equation 49x^2 = 81 - 81y^2,

The foci of the ellipse are:

`\text{(-}\frac{4\sqrt[]{2}}{7},\text{ 0), (}\frac{4\sqrt[]{2}}{7},\text{ 0)}`

The vertices of the ellipse are:

`(\text{-}(9)/(7),\text{ 0), }((9)/(7),\text{ 0)}`