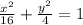We have the following trigonometric identity:
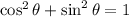
then, if we calculate the following expression:
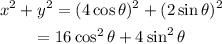
as we can see, the coefficients 16 and 4 gives us the lenght of the axis of the ellipse, therefore, the rectangular equation that eliminates the parameter is: