In order to answer this question, we must compute the products.
From left to right, we have

the second expression is
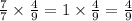
In the third expression, we must convert the mixed fraction form into a simple fraction form
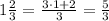
then, the product is given by
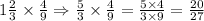
And the last expression is
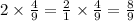
Then we have the following table:
now, we can use cross-multiplication to compare fractions and find out which is greater.
they both are in order. Now, lets compute the cross multiplication for the others:
Therefore, they are in the correct order.