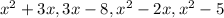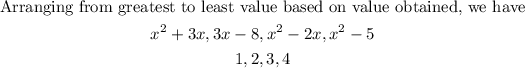
To find the average rate of change of a function within a given interval, we use the following formula;
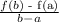
So for the first equation, we have;
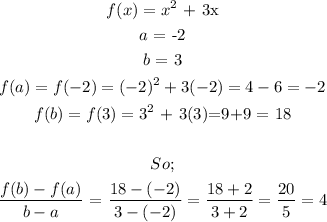
For the second equation, we have;
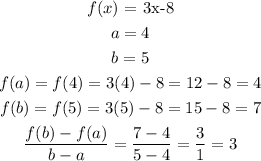
For the third equation, we have;
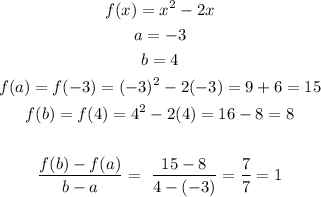
For the last equation, we have;
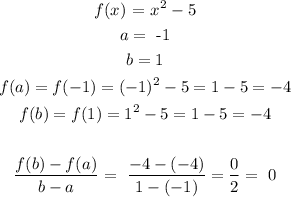
So arranging the functions from highest to lowest based on the value obtained, we have;