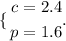Question

5c + 4p = 18.402c + 4p = 11.20

Answer 1

To solve the system of linear equations you can use the reduction or elimination method, like this

`\begin{gathered} \mleft\{\begin{aligned}5c+4p=18.40\text{ }\rightarrow\text{ multiply this equation by -1 to convert 4p to }-4p \\ 2c+4p=11.20\text{ }\end{aligned}\mright? \\ \end{gathered}`

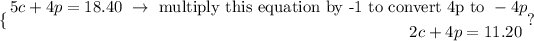
So,

`\mleft\{\begin{aligned}-5c-4p=-18.40 \\ 2c+4p=11.20\end{aligned}\mright.`

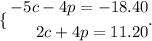
Now you can sum both equations and then you have

`\begin{gathered} -3c+0p=-7.2 \\ -3c=-7.2 \\ \text{Divide both sides of the equation by -3} \\ (-3c)/(-3)=(-7.2)/(-3) \\ c=2.4 \end{gathered}`

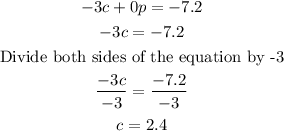
Now you can plug the value of c into any of the initial equations to get the value of p, for example in the second equation

`\begin{gathered} 2c+4p=11.20 \\ 2(2.4)+4p=11.2 \\ 4.8+4p=11.2 \\ \text{substract 4.8 from both sides of the equation} \\ 4.8+4p-4.8=11.2-4.8 \\ 4p=6.4 \\ \text{divide both sides of equation by 4} \\ (4p)/(4)=(6.4)/(4) \\ p=1.6 \end{gathered}`

Therefore, the solution of this system of equations is

`\mleft\{\begin{aligned}c=2.4 \\ p=1.6\end{aligned}\mright.`