ANSWER
a) n = 20m + 45
b) 105 dolls
c) 5 minutes
Step-by-step explanation
At noon, the elves had 45 dolls and they continued producing 20 dolls per minute.
a) We want to write an equation to model the situation.
This situation displays a linear relationship. The general form of a linear equation is:

where m = slope
b = y intercept
The slope is the rate of change of the y with respect to x. Relating that to the situation, the slope is the number of dolls the elves produce per minute.
That is 20 dolls.
Therefore:
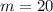
The y intercept represents the initial value of a function. For the situation given, the initial value of the dolls is 45.
Therefore:
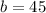
Therefore, the equation that models the number of dolls, n, with respect to minutes, m, is:
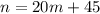
b) To find the number of dolls after 3 minutes, we have to find the value of n when m is 3.
That is:
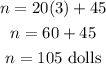
The number of dolls after 3 minutes is 105.
c) To find how long it takes them to make 145 dolls, we have to find the value of m when n is 145.
That is:

It would take 5 minutes for them to make 145 dolls.