saysWe want to find out whether;
![\frac{\sqrt[]{2}}{8}](https://img.qammunity.org/2023/formulas/mathematics/college/npvx4ekeqtw208b2pha5mvmylk32ofy5m4.png)
Is rational or irrational.
A condition for a number to be rational is for us to be able to write the number as a fraction, i.e in the form;

This is subject to some caveats;
p and q have to be integers, q has to be a non-zero denominator, i.e, it cannot be zero.
The number in question is;
![\frac{\sqrt[]{2}}{8}](https://img.qammunity.org/2023/formulas/mathematics/college/npvx4ekeqtw208b2pha5mvmylk32ofy5m4.png)
Student A argues that the number is rational because it is written as a fraction, however, the numerator is irrational, and therefore, the whole number is irrational.
Student B is says that the number is irrational because the numerator is irrational, this si correct, since we can express the number as;
![\frac{\sqrt[]{2}}{8}=\sqrt[]{2}*(1)/(8)](https://img.qammunity.org/2023/formulas/mathematics/college/f8t4p104w7d2107fuar46rnwaza4fla1hn.png)
and multiplying an irrational number with a rational number will always result in an irrational number.
We could see for example;
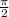
This is also a fraction, but since pi is irrational, the whole number is irrational.
Therefore, Student A is wrong and Student B is correct.