1 Answer

Ido Weinstein · Answer 1 · 2023-06-21T12:42:06+0000

ANSWER

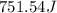
Step-by-step explanation

Parameters given:

Weight of merry-go-round, W = 822 N

Radius of merry-go-round, r = 1.95 m

Horizontal force, F = 69.3 N

Time, t = 3.61 s

Acceleration due to gravity, g = 9.8 m/s²

First, we have to find the inertia of the merry-go-round (solid cylinder):

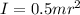
where m = mass; r = radius

We have that the mass of the merry-go-round is:

$\begin{gathered} W=mg \\ \Rightarrow m=(W)/(g)=(822)/(9.8) \\ m=83.88\operatorname{kg} \end{gathered}$

Therefore, the inertia is:

$\begin{gathered} I=0.5\cdot83.88\cdot1.95^2 \\ I=159.48\operatorname{kg}m^2 \end{gathered}$

Now, we can find the angular acceleration using the relationship between inertia and force:

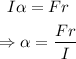
$\begin{gathered} I\alpha=Fr \\ \Rightarrow\alpha=(Fr)/(I) \end{gathered}$

Therefore, the angular acceleration:

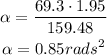
$\begin{gathered} \alpha=(69.3\cdot1.95)/(159.48) \\ \alpha=0.85rad\/s^2 \end{gathered}$

Now, we can find the angular velocity using:

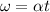
$\omega=\alpha t$

Therefore, the angular velocity is:

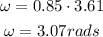
$\begin{gathered} \omega=0.85\cdot3.61 \\ \omega=3.07rad\/s \end{gathered}$

Now, we can find the kinetic energy of the merry-go-round using:

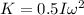
$K=0.5I\omega^2$
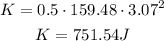
$\begin{gathered} K=0.5\cdot159.48\cdot3.07^2 \\ K=751.54J \end{gathered}$

That is the answer.

Please log in or register to add a comment.