Answer:
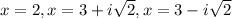
Explanation:
Given the function:
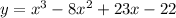
As seen on the graph, from the point (2,0) one of the roots of the function:

This means that x-2 is a factor of the polynomial y.
To get the other roots, first, divide y by x-2:
So, we have that:

We then solve the quadratic equation for the other roots of y:
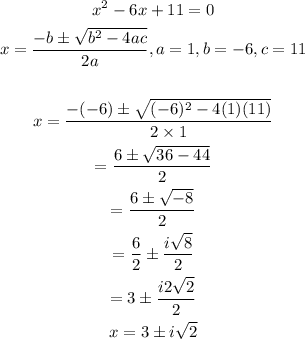
The other two roots of y are:
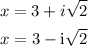
Thus, the exact roots of y are:
