To answer this, we will find the equation of the line that passes through point C and D and check which option is in the same line, this will be the answer.
First, let's find the slope using th coordinates of the points C and D:
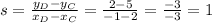
Now, we can use point C, for example, to right in the slope-point form:
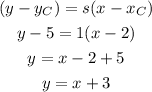
With this equation, we can input values of x and check is we get the same y.
Alternative A and C have x = 0, so let's check it:
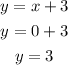
I got y = 3, neither alternative have y = 3, so it isn't A nor C.
B and D have x = 1, let's check it:
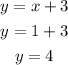
We got y = 4, which matches alternative D.
So, the correct alternative is D.