Question

Plot the points with polar coordinates (-5,-7pi/6) and (3,3pi/4) using the pencil

Answer 1

Each circle corresponds to a different value of r (the first coordinate, on the left).

And each line segment emanating from the center corresponds to a different value of θ (second coordinate, on the right).

Also, we need to know that a negative value of θ corresponds to the angle 2π - θ.

Furthermore, if r is negative, we need to plot the point opposite by the center to the point (-r, θ).

So, let's begin by plotting the point

`(-5,-(7\pi)/(6))`

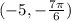
Since the second entry is negative, it corresponds to the angle:

`2\pi-(7\pi)/(6)=(12\pi-7\pi)/(6)=(5\pi)/(6)`

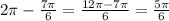
Also, since the first entry is negative, we need to plot the point on the circle corresponding to r = 5, but in the opposite direction of the ray corresponding to the angle 5π/6:

Now, the second point is

`(3,(3\pi)/(4))`

For this point, both coordinates are positive. So, we need to plot it (red point below) on the circle corresponding to r = 3, and on the ray corresponding to θ = 3π/4: