Let x be the number.
We know that we squared ir and doubled it, this means:
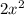
This have to be equal to four more than the product of seven and the number:
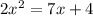
this is the same as:
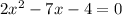
this can be solved for the general formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
in our case a=2, b=-7 and c=-4; then:
![\begin{gathered} x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4(2)(-4)}}{2(2)} \\ x=\frac{7\pm\sqrt[]{49+32}}{4} \\ x=\frac{7\pm\sqrt[]{81}}{4} \\ x=(7\pm9)/(4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kg370blidjrx5xsl8h6um3iwnaoyezcksz.png)
hence:
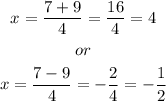
Since we are looking for a whole number, then the number is 4.