The amount of money A in an account after t years of investing a principal P at a rate r compounded continuously, is:
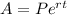
To find the value P that he must pay now so that the amount of money will be equal to $5000 in 6 years at a rate of 2.5% per year, isolate P and substitute A=5000, r=2.5/100 and t=6:
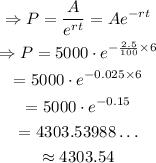
Therefore, he paid $4303.54.