Question

1.A ball is thrown from a stadium 45m above the ground with a horizontal velocity of5.7m/s.a) How long does it the ball to hit the ground below?b) How far from the base of the stadium will the ball land?

Answer 1

Given data:

* The height of the stadium is 45 m.

* The horizontal velocity of the ball is 5.7 m/s.

Solution:

By the kinematics equation, the vertical motion of the ball is,

`H=u_yt+(1)/(2)gt^2`

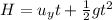
where H is the height, g is the acceleration due to gravity, u_y is the vertical initial velocity, and t is the time taken,

The vertical initial velocity of the ball is zero.

Substituting the known values,

`\begin{gathered} 45=0+(1)/(2)*9.8* t^2 \\ 45=4.9* t^2 \\ t^2=(45)/(4.9) \\ t^2=9.2 \\ t=3.03\text{ s} \end{gathered}`

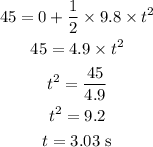
Thus, the time taken by the ball to hit the ground is 3.03 seconds.

(b). By the kinematics equation, the horizontal motion of the ball is,

`R=u_xt+(1)/(2)at^2`

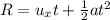
where u_x is the horizontal initial velocity, a is the acceleration, and R is the horizontal range,

The acceleration of the ball in the horizontal direction is zero.

Substituting the known values,

`\begin{gathered} R=5.7*3.03+0 \\ R=17.27\text{ m} \end{gathered}`

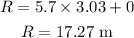
Thus, the ball will land 17.27 meter from the base of stadium.