Question

Would just like to clarify my that answer is correct

Answer 1

309.2 ft

Step-by-step explanation:

We can represent the situation with the following figure

So to find the height from the car to the plane, we need to find the values of x and y using the formed triangles.

To find the value of x, we will use the trigonometric function tangent as follows

`\tan 52=(x)/(150)`

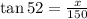
Because x is the opposite side of the angle of 52 degrees and 150 is the adjacent side.

Then, solving for x, we get:

`\begin{gathered} x=150\cdot\tan 52 \\ x=150\cdot1.28 \\ x=192\text{ ft} \end{gathered}`

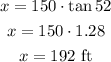
In the same way, we can calculate the value of y as follows

`\begin{gathered} \tan 38=(y)/(150) \\ y=150\cdot\tan 38 \\ y=150\cdot0.78 \\ y=117.2\text{ ft} \end{gathered}`

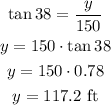
Therefore, the answer is

x + y = 192 ft + 117.2 ft = 309.2 ft

So, the plane is 309.2 ft above the car.