The ratio of scale model of a boat to a real boat is
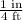
Part A:
Using that ratio, if the height of the real boat is 28 feet, then we can solve it by
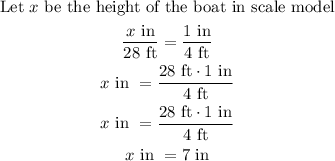
Therefore, the height of the boat in scale model is 7 inches.
Part B:
Using the same method as above, we have the following

Therefore, the length of the real boat is 20 feet.