Question

I want to see if I did a problem right

Answer 1

The given function is:

`t=((2d)/(g))^{(1)/(2)}`

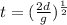
Where t is the time it takes for the object to reach the ground (in seconds), d is the initial distance (in feet) above the ground level, and the constant g=32 ft/s².

It is given that the initial distance is 25 feet, and it is required to find the time it takes for the object to reach the ground.

To do this, substitute the given values into the formula provided, and solve the equation for t.

Substitute d=25, g=32 into the formula:

`t=((2(25))/(32))^{(1)/(2)}`

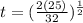
Solve the equation for t:

`\Rightarrow t=(\frac{\cancel{2}^1(25)}{\cancel{32}_(16)})^{(1)/(2)}=((25)/(16))^{(1)/(2)}`

Apply the quotient property of powers:

`\Rightarrow t=\frac{25^{(1)/(2)}}{16^{(1)/(2)}}=\frac{\sqrt[]{25}}{\sqrt[]{16}}=(5)/(4)=1(1)/(4)\text{ seconds}`

Hence, the required time is t=1 1/4 seconds or 1.25 seconds.