We have to calculate the probability of pulling three candies in a row (without replacement).
We can think of each draw as a different event.
As there is no replacement of the candies, the probability changes with the result of the previous event.
We have 12+12+7+13+3+10 = 57 candies in the bag.
The probability of pulling a brown candy in the first draw is 13/57, as 13 of the candies are brown.
Now, for the second draw, the probability of picking a brown candy is 12/56, as we have one less candy and it is the brown one we picked in the first draw.
Lastly, we have a probability of 11/55 of picking a third brown candy from the bag.
Then, the probabiltiy of 3 brown candies in a row is the product of the probabilities of these three events:

Answer: the probability of drawing 3 brown candies in a row without replacement is 13/1330.
NOTE:
If the last candy is green, then we have to change the third event.
The first two draw will remain the same, but the probabilty of drawing a green candy in the third draw will be 7/55, as 55 candies are left in the bag and 7 of them are green.
We then can calculate the probability of the two first candies being brown and the third being green as:
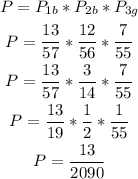
Answer: the probability of the first two draws being a brown candy and the third being a green candy is 13/2090.