Since the account is under a compounded interest, we need to apply the following expression in order to determine the final amount:

Where A is the final amount, P is the initial principal, r is the interest rate, n is the number of times it get compounded in a year and t is the elapsed time.
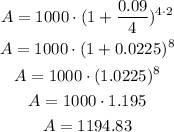
They will be able to spend $1194.83