Question

determine the total force and the absolute pressure on the bottom oa a swimming pool 28.0m by 8.5 whose uniform depth is 1.8m. what will be the pressure against the side of the side of the pool near the bottom

Answer 1

First, consider that the preassure of a column of water is given by:

`P=\rho gh`

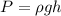
where:

ρ: water density = 1000kg/m^3

g: gravitational acceleration constant = 9.8m/s^2

h: depth of the pool = 1.8m

Replace the previous values of the parameters into the formula for P:

`P=(1000(kg)/(m^3))(9.8(m)/(s^2))(1.8m)=17640(N)/(m^2)`

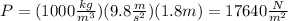
Now, consider that the surface area of the pool is:

`A=(28.0m)(8.5m)=238m^2`

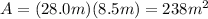
Then, the total force on the bottom is:

`F=P\cdot A=(17640(N)/(m^2))(238m^2)=4,198,320N`

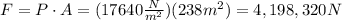
Now, consider that the absolute pressure depends if you take into account the atmospheric pressure or not.

If you consider the atmospheric pressure, then, the absolute pressure is the sum of the pressure due to the water of the pool and the pressure of the atmospheric pressure. Then:

absolute pressure = 101,325N/m^2 + 17,640N/m^2 = 118,965N/m^2

If the atmospheric pressure is not taken into account the absolute pressure is 17,640N/m^2.

Pressure in any direction (i.e. on the wall) very near the bottom will be nearly the same as at the bottom.