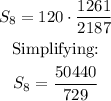Question

I need help with this practice problem in my trigonometry prep book.

Answer 1

Sum of the First n Terms of a Geometric Sequence

Given a geometric sequence (or series) with a first-term a1 and common ratio r, the sum of the first n terms is given by:

`S_n=a_1\cdot(1-r^n)/(1-r)`

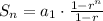
We are given the series:

`120-80+(160)/(3)-(320)/(9)+\cdots`

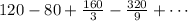
Before calculating the required sum, we need to find the common ratio. It's defined as the division of two consecutive terms. For example, using the first two terms:

`\begin{gathered} r=-(80)/(120) \\ Simplify\colon \\ r=-(2)/(3) \end{gathered}`

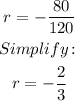
The first term is a1 =120. Now apply the formula:

`S_8=120\cdot(1-(-(2)/(3))^8)/(1+(2)/(3))`

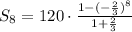
Operating:

`\begin{gathered} S_8=120\cdot(1-(2^8)/(3^8))/((5)/(3)) \\ S_8=120\cdot(1-(256)/(6561))/((5)/(3)) \\ S_8=120\cdot((6561-256)/(6561))/((5)/(3)) \\ S_8=120\cdot((6305)/(6561))/((5)/(3)) \end{gathered}`

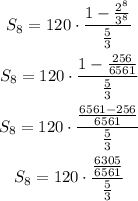
Calculating:

`\begin{gathered} S_8=120\cdot(1261)/(2187) \\ \text{Simplifying:} \\ S_8=(50440)/(729) \end{gathered}`