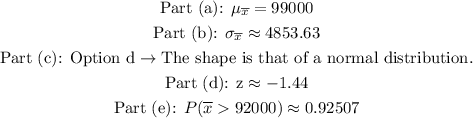Question

The average salary for a certain profession is 599,000. Assume that the standard deviation of such salaries is $35,000. Consider a random sample of 52 people in this profession and let x represent the mean salaryfor the sampleClick the icon to view the table of normal curve areas.a.What is wab.What is o;?c0:- (Round to two decimal places as needed.)Describe the shape of the sampling distribution of XOA. The shape is that of a uniform distribution.OB. The shape is that of a binomial distributionOC. The shape is that of a poisson distributionOD. The shape is that of a normal distributionFind the Z-score for the value x=92,000z=(Round to two decimal places as needed.)e. Find P(x>92.000)d.Click to elect Unswers

Answer 1

For part (a), we are looking for the mean of population. This is the same as the average of the population.

`\mu_{\overline{x}}=99000`

For part (b), the mean of the standard deviation of the population is being asked. The formula is as follows.

`\begin{gathered} \sigma_{\overline{x}}=\frac{\sigma}{\sqrt[]{n}} \\ =\frac{35000}{\sqrt[]{52}} \\ \approx(35000)/(7.211102551) \\ \approx4853.6267 \\ \approx4853.63 \end{gathered}`

For part (c), since the sample size is greater than 30, which is 52, the shape must be normally distributed.

For part (d), the z-score formula is as follows.

`\begin{gathered} z=\frac{\overline{x}-\mu_{\overline{x}}}{\sigma_{\overline{x}}} \\ \approx(92000-99000)/(4853.6267) \\ \approx(-7000)/(4853.6267) \\ \approx-1.4422 \\ \approx-1.44 \end{gathered}`

For part (e), to obtain the given probability, look at the z-score table.

The one shown in table is the probability less than or equal to the given mean, 92000. Thus, if we want to obtain the probability higher than 92000, we need to subtract the obtained probability from 1. This is because the sum of all the probabilities is equal to 1.

`\begin{gathered} P(\overline{x}>92000)=1-P(\overline{x}\le92000) \\ \approx1-0.07493 \\ \approx0.92507 \end{gathered}`

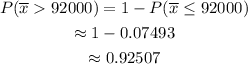
To summarize, the answer for each part is as follows.

`\begin{gathered} \text{Part (a): }\mu_{\overline{x}}=99000 \\ \text{Part (b): }\sigma_{\overline{x}}\approx4853.63 \\ \text{Part (c): Option d}\rightarrow\text{The shape is that of a normal distribution.} \\ \text{Part (d): z}\approx-1.44 \\ \text{Part (e): }P(\overline{x}>92000)\approx0.92507 \end{gathered}`