Polynomials
A polynomial of degree 3 can be written in factor form as follows:
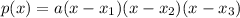
Where x1, x2, and x3 are the zeros of the polynomial, and a is the leading coefficient.
We are given the three zeros: x1= -8, x2 = -8, x3 = 6
Note we have repeated the root -8 because it has a multiplicity of 2.
Substituting these values, we have:
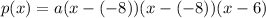
Operating:
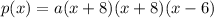
We can set the value of a to any non-zero real number. If a=1, our polynomial is:
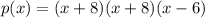
For a=-2, we have:
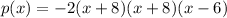
We have given two different solutions, and you can give more by changing the value of a.