Recall that the given function jumps at the value of x=1. To values that are on the left of 1 (x<=1) the function that is applied is a straith line, different to the line applied to values of x greater than 1. Note that when we replace x by 1 in the function, we should get 1. Also, note that for values greater than 1, but really close, the values of the function approach the number 3.
So, to identify which of the options is the correct, we simply take a look at the given line equations, and then evaluate it at x=1. The line applied to the values less than or equal to 1, by replacing x by 1, we should get the value of 1. And for the line applied to the values greater than 1, by replacing x by 1, we should get 3.
In the first option, the line applied to values less than 1 is -x+1. If we replace x by 1, we get -(1)+1 =0. So this option is discarded .
We can do the same for the rest options as follows:
- line 3x-1. Evaluating at x=1, we get 3(1)-1 = 2
- line 3x-1 . Evaluating at x=1, we get 3(1)-1 = 2
- line 3x-2. Evaluating at x=1, we get 3(1)-2=1
So the candidate for a solution is the last option. We confirm this by taking the line applied to the values greater than 1 (x+2) and evaluating it at x=1. We should get the value of 3.
Note that
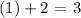
So the correct answer is indeed the last one.