Step-by-step explanation
Since we have the given quadratic function:
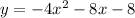
a)
Since the value of the squared term coefficient is negative, thus the graph opens up.
b)
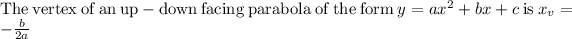
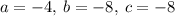
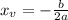
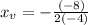
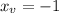
Plugging in the x_v value into the equation:
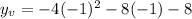
Computing the powers:

Multiplying numbers:
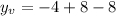
Adding numbers:
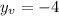
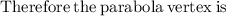
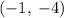
c) For a quadratic equation of the form ax^2 + bx + c = 0 the discriminant is b^2 -4ac
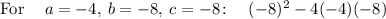
Computing the powers and multiplying numbers:
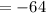
Since the discriminant cannot be negative, there are not x-intercepts.
d) Identifying y-intercepts:
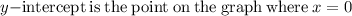
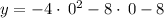
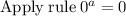
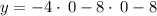
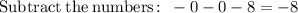
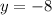
The y-intercept is at (0,-8)