Given the equation of a circle:
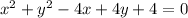
Let's find the center of the circle, (h, k).
To find the center of the circle, rewrite the equation in standard form:

Where:
(h, k) is the center.
Rewrite the equation:
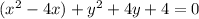
Complete the square for the two groups:
x²-4x and y²+ 4y.
Apply the formula:
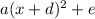
Now, we have the following:
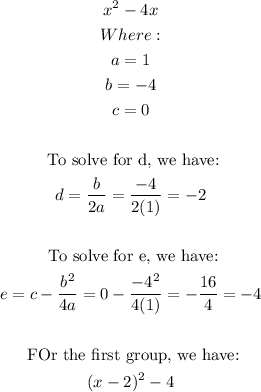
Complete the square for the second group:

Now, combine the expressions in the original equation

Combine like terms and move the constants to the right side of the equation:

Therefore, the equation of the circle in standard form is:
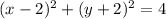
Where:
h = 2
k = -2
Therefore, the center of the circle is:
(h, k) ==> (2, -2)
ANSWER:
(2, -2)