The given expression is
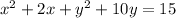
First, we divide the coefficients 2 and 10 by 2, then we find their square power
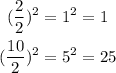
We add 25 and 1 to each side of the equation
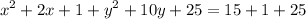
Now, we factor both trinomials
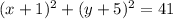
Where h = -1 and k = -5. So, the center is C(-1, -5).
The radius would be
![\begin{gathered} r^2=41 \\ r=\sqrt[]{41}\approx6.4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/im93qx9gcf1vvj213aiu2qrw67qwjo2wd9.png)
The radius is 6.4 units long.