Question

At the gift shop, they sell small greeting cards and large greeting cards. The cost of asmall greeting card is $1.70 and the cost of a large greeting card is $3.65. How muchwould it cost to get 3 small greeting cards and 5 large greeting cards? How muchwould it cost to get x small greeting cards and y large greeting cards?

Answer 1

Lets x be the number of small greeting cards and y the number of large greeting cards, the cost would be the sum of the quantity by the price of each type of cards.

Then, we can write:

`\begin{gathered} \text{Cost}=\text{Cost of small cards+Cost of large cards} \\ \text{Cost}=1.70\cdot x+3.65\cdot y \end{gathered}`

Then, if we get 3 small cards and 5 large cards we can calculate the cost as:

`\begin{gathered} \text{Cost}=1.70\cdot3+3.65\cdot5 \\ \text{Cost}=5.10+18.25 \\ \text{Cost}=23.35 \end{gathered}`

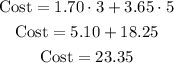
Answer:

a) The cost of 3 small cards and 5 large cards is $23.35.

b) We can write the cost as C = 1.70*x + 3.65*y