Question

Given that f(x) = 2^x and g(x) = x ^ 2 , answer the questions that follow. a. Your friend claims the graph of f(x) = 2 ^ x increases at a faster rate than the graph of g(x) = x ^ 2 Is your friend correct? Explain your reasoning.b. How are the 2 functions different?

Answer 1

GIven:

The objective is to find whether f(x) =2^x increases at a faster rate than the graph of g(x) = x^2.

Consider x = 0, 1, 2, 3, 4.

In f(x), substitute the values of x.

`\begin{gathered} f(1)=2^1=2 \\ f(2)=2^2=4 \\ f(3)=2^3=8 \\ f(4)=2^4=16 \\ f(0)=2^0=1 \end{gathered}`

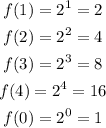
Now, substitute the values of x in g(x).

`\begin{gathered} g(1)=1^2=1 \\ g(2)=2^2=4 \\ g(3)=3^2=9 \\ g(4)=4^2=16 \\ g(0)=0^2=0 \end{gathered}`

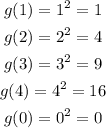
By comparing the coordinates of both the grpah of f(x) and g(x), we observed equal rate of increase.

Let's compare the graph of both equations.

Here, blue graph represents y=2^x and red graph represents y=x².

Since we obtained graphs which are almost increasing at the same rate upto x= 16 and then f(x)=2^x starts increasing in a faster rate.

Hence, it is correct that the graph of f(x) is increasing at a faster rate after x= 16.