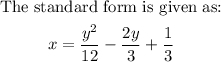SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given data
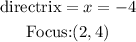
STEP 2: Write the equation of a parabola
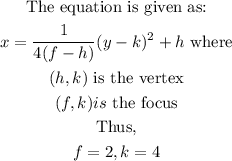
STEP 3: Get the value of h
The distance from the focus to the vertex is equal to the distance from the vertex to the directrix. Therefore:
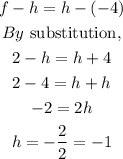
STEP 4: Get the standard form of equation
Hence, the standard form becomes: