Question

The two figures are similar. Write the similarity statement. Justify your answer using factor and showing all work. Describe (in general since it isn't on a graph) the transformations from ABC to the new figure. First Triangle A to B: 40 B to C: 60 C to A: 50 Second TriangleX to Y: 31.25 Y to Z: 25 Z to X: 37.5

Answer 1

If two figures are similar, all of their pairs of corresponding sides have the same ratio:

To prove if the given figures are similar find the ratio between corresponding sides (to identify corresponding sides start with the smaller side in both figures and follow this logic):

`\begin{gathered} (AB)/(YZ)=(40)/(25)=1.6 \\ \\ (AC)/(YX)=(50)/(31.25)=1.6 \\ \\ (BC)/(ZX)=(60)/(37.5)=1.6 \end{gathered}`

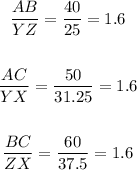
As the ratio between corresponding sides is the same (1.6); triangle ABC is similar to traingle YZX

Transformations from ABC to YZX: ABC (preimage) is dilated to get YZX (Image)

Find the factor of dilation:

`\begin{gathered} Fd=(Image)/(Preimage) \\ \\ Fd=(YZ)/(AB)=(25)/(40)=(5)/(8) \end{gathered}`

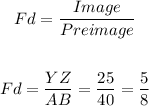
Then, the transformation from ABC to YZX is a dilation with a factor of 5/8