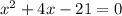Work backwards to write a quadratic equation that will have solutions of x = 3 and x = -7

Question

asked Nov 13, 2023 182k views

1 Answer

Novitzky · Answer 1 · 2023-11-19T05:51:31+0000

Given:

There are given that the solutions of x are 3 and -7.

Step-by-step explanation:

From the given value of x,

$\begin{gathered} x-3=0\text{ and} \\ x+7=0 \end{gathered}$

Then, two binomials that make up the quadratic are:

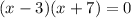
Then,

Solve the above factor:

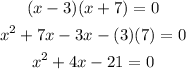
$\begin{gathered} (x-3)(x+7)=0 \\ x^2+7x-3x-(3)(7)=0 \\ x^2+4x-21=0 \end{gathered}$

Final answer:

Hence, the quadratic equation is shown below;