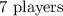Question

the following table lists the ages and number of players per age group that are on a football team. Let A= (football players who are older than 9 years old) how many players are in the complement of A?

Answer 1

the number of players that are in the complement of A is;

`7\text{ players}`

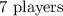
Given the table in the attached image.

A = (football players who are older than 9 years old)

`\begin{gathered} n(A)=6+2 \\ n(A)=8 \end{gathered}`

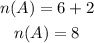
the compliment of A are the values that are not in A;

`\begin{gathered} n(A^(\prime))=n(8)+n(9)=5+2_{} \\ n(A^(\prime))=7 \end{gathered}`

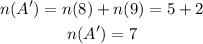
Therefore, the number of players that are in the complement of A is;

`7\text{ players}`